Wolfram Model Training Course: Difference between revisions
No edit summary |
No edit summary |
||
| (6 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[File:CA Shell Transparent.png|frame|right|100px|A seashell found by Hartlabs, that produces a cellular automata pattern.]] An introduction to and conceptually focused walkthrough of the Wolfram Model framework in it’s entirety, serving as a gateway to its materials and resources spread across the internet, for beginners, enthusiasts, and experts alike. | |||
NOTE : WORK IN PROGRESS | NOTE : WORK IN PROGRESS | ||
== '''Part 1 : Prerequisites''' == | == '''Part 1 : Prerequisites''' == | ||
| Line 10: | Line 30: | ||
=== [https://www.youtube.com/watch?v=ZPbYriK_gCs Isomorphism] & [https://www.youtube.com/watch?v=hVerxuP4cFg Graph Isomorphism]=== | === [https://www.youtube.com/watch?v=ZPbYriK_gCs Isomorphism] & [https://www.youtube.com/watch?v=hVerxuP4cFg Graph Isomorphism]=== | ||
An isomorphism is an equivalence relation between different objects, structures, or systems, proven through a structure-preserving mapping. It ensures that operations, relationships, and transformations in one structure correspond directly to those in another. | An isomorphism is an equivalence relation between different objects, structures, or systems, proven through a structure-preserving mapping. It ensures that operations, relationships, and transformations in one structure correspond directly to those in another. | ||
[[File:Transformations (small).gif|right|frame|100px|Depiction of mathematical transformations by Raibatak Das.]] | |||
=== [https://www.youtube.com/watch?v=YD3HIMUae_4 Transformations] === | === [https://www.youtube.com/watch?v=YD3HIMUae_4 Transformations] === | ||
| Line 40: | Line 62: | ||
[[File:4 classes of behavior.png|center|frame|100px]] | [[File:4 classes of behavior.png|center|frame|100px|The four classes of behavior that rules typically fall into : homogenous, patterned, random and complex. From Stephan Wolfram, A New Kind of Science.]] | ||
The second arc of the book is spent making connections between computational rules and how they show up in nature, in system analysis and in fundamental physics. | The second arc of the book is spent making connections between computational rules and how they show up in nature, in system analysis and in fundamental physics. | ||
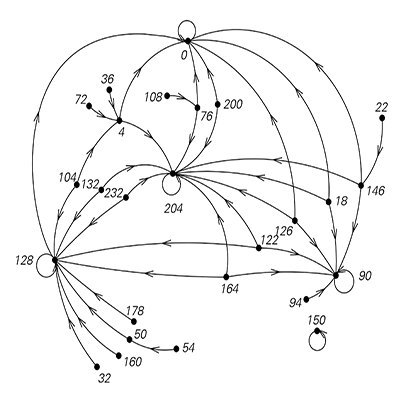
[[File:CA Emulation Map.png|right|frame|100px]] | [[File:CA Emulation Map.png|right|frame|100px|A map of rule emulations of other rules. From Stephan Wolfram A New Kind of Science.]] | ||
The third and final arc of the book is spent formalizing the observations made in these experiments, by first showing the Elementary Cellular Automata Rule Class emulating each other under different initial conditions. Wolfram and Cook then prove the universality of Rule 110, strongly implying that any rule within this rule class, when given the right initial conditions can lead to an emulation of Rule 110, therefore proving the entire rule class as Turing Universal. | The third and final arc of the book is spent formalizing the observations made in these experiments, by first showing the Elementary Cellular Automata Rule Class emulating each other under different initial conditions. Wolfram and Cook then prove the universality of Rule 110, strongly implying that any rule within this rule class, when given the right initial conditions can lead to an emulation of Rule 110, therefore proving the entire rule class as Turing Universal. | ||
| Line 87: | Line 107: | ||
The Ruliad is “the entangled limit of all possible rules” and is the most important "true ontology" of the wolfram model. So to conduct faithful science, we study our interface with this object. | The Ruliad is “the entangled limit of all possible rules” and is the most important "true ontology" of the wolfram model. So to conduct faithful science, we study our interface with this object. | ||
[[File:Ruliad Approximation.png|right|frame|100px]] | [[File:Ruliad Approximation.png|right|frame|100px|A finite approximation to the Ruliad. From Stephan Wolfram in "The Concept of the Ruliad."]] | ||
Some properties of the Ruliad are that it is maximally symmetric and countably infinite. From the perspective of the entire object you can think of all mappings as bijective (one-to-one), but for all systems within the Ruliad, all mappings are surjective. In other words, subsystems embedded in this object cannot perceive it without consolidating information about its structure. This will play an important role in observer theory and, subsequently, the Wolfram Model of Physics. | Some properties of the Ruliad are that it is maximally symmetric and countably infinite. From the perspective of the entire object you can think of all mappings as bijective (one-to-one), but for all systems within the Ruliad, all mappings are surjective. In other words, subsystems embedded in this object cannot perceive it without consolidating information about its structure. This will play an important role in observer theory and, subsequently, the Wolfram Model of Physics. | ||
| Line 107: | Line 127: | ||
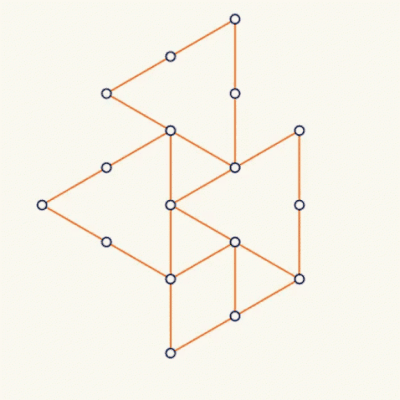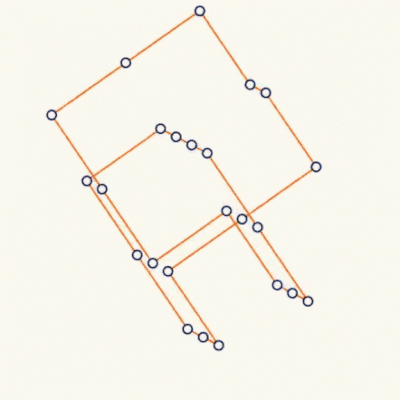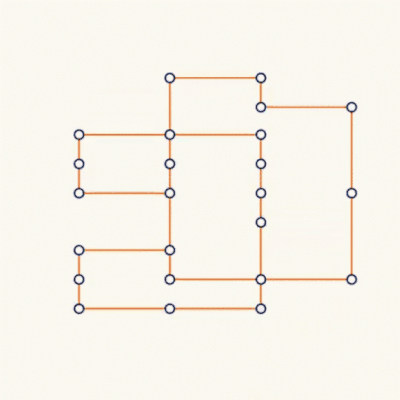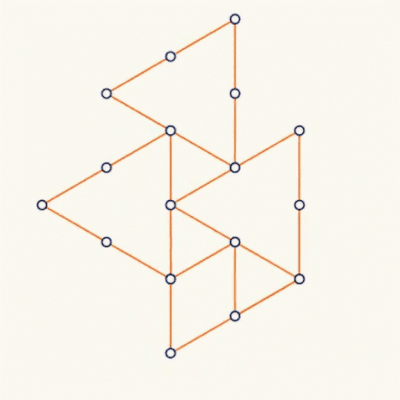
This animation to the right illustrates these limitations. | This animation to the right illustrates these limitations. | ||
[[File:Rotating Object.gif|right|frame|500px|]] | [[File:Rotating Object.gif|right|frame|500px|Animation of a rotating object by Clayton Shonkwiler.]] | ||
===Perception=== | ===Perception=== | ||
| Line 160: | Line 180: | ||
Taking the XY -> XYZ example again, we must force the constraint that XY needed to happen before XYZ happens, since XYZ depends on XY, for an observer that can only see a finite number of these operations occur at a time. | Taking the XY -> XYZ example again, we must force the constraint that XY needed to happen before XYZ happens, since XYZ depends on XY, for an observer that can only see a finite number of these operations occur at a time. | ||
[[File: | [[File:Relativity of Simultaneity.gif|right|frame|300px|An animation illustrating relativity of simultaneity.]] | ||
In the large limit, this structure forms the notion of directed time (causality) for an observer: That in order for an event to happen, a previous event must have had already happened. We also start to see how this ambiguity in the structure from an observer's perspective creates the notion of relativity : That if we have two or more of these operations that occur in two different places, say XY -> XYZ over here, and XY - XYZ over there, we have to perceive these in a causal order…where one of those events has to come prior to the other one, and that, depending on where you are embedded in this evolution determines which one happened for them first! ([https://en.wikipedia.org/wiki/Relativity_of_simultaneity Relativity of Simultaneity]) | In the large limit, this structure forms the notion of directed time (causality) for an observer: That in order for an event to happen, a previous event must have had already happened. We also start to see how this ambiguity in the structure from an observer's perspective creates the notion of relativity : That if we have two or more of these operations that occur in two different places, say XY -> XYZ over here, and XY - XYZ over there, we have to perceive these in a causal order…where one of those events has to come prior to the other one, and that, depending on where you are embedded in this evolution determines which one happened for them first! ([https://en.wikipedia.org/wiki/Relativity_of_simultaneity Relativity of Simultaneity]) | ||
| Line 245: | Line 265: | ||
Reading a book in less than a few seconds as if it were like a painting on the wall, is like a super power, a term Wolfram often implies when discussing this paradigm. Computationally Irreducible processes contain a lot of power (arguably, the power of the entire universe), because it is the ability to program any system, to compute any computable function: | Reading a book in less than a few seconds as if it were like a painting on the wall, is like a super power, a term Wolfram often implies when discussing this paradigm. Computationally Irreducible processes contain a lot of power (arguably, the power of the entire universe), because it is the ability to program any system, to compute any computable function: | ||
If we want machine learning to be able to do the best it can, and perhaps give us the impression of “achieving magic”, then we have to allow it to show computational irreducibility. | ''"If we want machine learning to be able to do the best it can, and perhaps give us the impression of “achieving magic”, then we have to allow it to show computational irreducibility."'' | ||
Excerpt from : [https://www.youtube.com/watch?v=7BgoJChzb_0 Stephen Wolfram Readings: What’s Really Going On in Machine Learning? Some Minimal Models] - Stephen Wolfram | Excerpt from : [https://www.youtube.com/watch?v=7BgoJChzb_0 Stephen Wolfram Readings: What’s Really Going On in Machine Learning? Some Minimal Models] - Stephen Wolfram | ||
Latest revision as of 22:54, 13 July 2025

An introduction to and conceptually focused walkthrough of the Wolfram Model framework in it’s entirety, serving as a gateway to its materials and resources spread across the internet, for beginners, enthusiasts, and experts alike.
NOTE : WORK IN PROGRESS
Part 1 : Prerequisites
Before diving into the work of Stephen Wolfram, the Wolfram Physics Project, or most projects from the Wolfram Institute, it's helpful to have some background knowledge in certain fields and concepts. If you're unfamiliar with these terms, below are some helpful video links and concise definitions.
Complex Systems
A basic introduction to complexity theory, covering network graphs and how those are used to model systems.
Isomorphism & Graph Isomorphism
An isomorphism is an equivalence relation between different objects, structures, or systems, proven through a structure-preserving mapping. It ensures that operations, relationships, and transformations in one structure correspond directly to those in another.
Transformations
A transformation is an operation that changes an object, structure, or system from one form or state to another. Such operations are called mappings or functions and can include translation, rotation, scale, reflection. In physics, the preservation of an object's structure under transformation proves invariance, meaning physical laws remain unchanged under different transformations.
Invariance
Invariance is the property that an object, structure, or system remains unchanged under transformations. In physics, invariance means that despite changes in form, position, or other aspects, specific properties or laws stay the same.
Turing Machines
The Turing machine is a construct invented by Alan Turing, capable of computing all computable functions. It is the basis for today's modern computer.
Turing Universality
The idea that something (typically a scripting language) is capable of computing any computable function. To prove that a system is Turing Universal, one must show that the system can emulate a Turing Machine.
Halting Problem
A famous contradiction proof by Alan Turing : that a Universal Truth Machine, a machine that can tell when a program will continue forever or halt, is impossible to construct and can not exist.
Godel Incompleteness
Explains the importance of Consistency, Decidability, and completeness in formal systems, and the history of Hilberts Program vs Godel’s Program and how Hilberts program [A complete, decidable and consistent theory of mathematic] was shown to be false.
Part 2 : New Kind of Science
A New Kind of Science, a book written by Stephan Wolfram in the 1980’s and published in 2002 set the foundations of the Wolfram Model. The book is split into three distinct arcs:
The first arc is a set of experiments where Wolfram exhaustively runs classes of rules, making general observations about their behaviour. He observers three key properties about these systems:
- That many simple rules can perform arbitrarily complicated behaviour, specifically behaviour that can not be described by mathematical equations.
- That rules typically fall into 4 classes of behaviour : Homogenous, Patterned, Random and Complex.
- That rules can emulate the behaviour of other rules.

The second arc of the book is spent making connections between computational rules and how they show up in nature, in system analysis and in fundamental physics.
The third and final arc of the book is spent formalizing the observations made in these experiments, by first showing the Elementary Cellular Automata Rule Class emulating each other under different initial conditions. Wolfram and Cook then prove the universality of Rule 110, strongly implying that any rule within this rule class, when given the right initial conditions can lead to an emulation of Rule 110, therefore proving the entire rule class as Turing Universal.
Computational Equivalence
In the Final Chapter, Wolfram poses this as strong evidence for The Principle of Computational Equivalence : That practically any system that follows rules, are computationally equivalent to a Turing universal machine, capable of computing any computable function.
“The answer is the Principle of Computational Equivalence, which states that, in effect, most rules will be equivalent in their computational capabilities—and in particular they will be capable of universal computation, so that any given rule can always “run a program” that will make it emulate any other rule.”
Excerpt from : The Concept of the Ruliad - Stephen Wolfram
Computational Irreducibility
The Principle of Computational Equivalence then gives explanatory power to The Phenomenon of Computational Irreducibility, explaining why many rules fail to be described by mathematical equations : Trying to predict or condense what a system following rules will do, is as hard as trying to solve the halting problem, and therefore one can not construct a universal truth machine that always gives us the answer. Operationally, a system can under different initial conditions emulate arbitrarily complicated rules and therefore to describe what they do, is nothing short of “they do everything.”
Computational Reducibility
In the same vein, Computational Reducibility also takes form: Since all systems are capable of computing any computable function under Computational Equivalence, then, there is also an infinite number of different patterns and regularities that these systems have access to. This feature forms the basis for doing science and mathematics.
These three ideas are core to understanding the Wolfram Model and will play major roles in practically every aspect of it, from the Ruliad, to Observer Theory, Multi-Computation and Ruliology.
In-Depth
I personally recommend watching the 16 part lecture series Wolfram made on the book, because he explains things with his point of view 20 years after its release, in the context of the 2020 Physics Model.
A New Kind of Science
Part 3 : The Ruliad
The work of A New Kind of Science and the Principle of Computational Equivalence tells us that systems can emulate each other's behavior and, therefore, all perform computations as sophisticated as any other arbitrarily complicated system, which also makes them as sophisticated as a Turing universal machine. In some sense, we can state colloquially that all systems are just this single Turing machine.
To dig deeper into this, we can ask a logical question: If a single rule can compute the universe, and all rules are computationally equivalent to each other, then does it actually matter what rule the universe is running on? Why would it be running on this rule over here rather than that rule over there? The logical conclusion to this is that the universe isn’t just running any single rule—it is running all possible rules. What exists is not a collection of separate systems or particular rules; rather, what actually exists is this abstract Turing Machine space of all possible rules.
Imagine we successfully identify a rule that describes everything about our universe. Then the obvious next question will be: “Why this rule, and not another?” Well, how about if actually the universe in effect just runs every possible rule? What would this mean? It means that in a sense the “full story” of the universe is just the ruliad.
Excerpt from : The Concept of the Ruliad - Stephen Wolfram
So when we look at any system, we aren’t really looking at just the system itself—we are looking at something deeper. Something we can’t fully see. We are looking at this Ruliad object: a very thin slice, a sample, a limited perception of it.
Properties
The Ruliad is “the entangled limit of all possible rules” and is the most important "true ontology" of the wolfram model. So to conduct faithful science, we study our interface with this object.
Some properties of the Ruliad are that it is maximally symmetric and countably infinite. From the perspective of the entire object you can think of all mappings as bijective (one-to-one), but for all systems within the Ruliad, all mappings are surjective. In other words, subsystems embedded in this object cannot perceive it without consolidating information about its structure. This will play an important role in observer theory and, subsequently, the Wolfram Model of Physics.
Rulial Space
Another way to think about the Ruliad is like a state-space “made” of rules, such that every coordinate in that space is occupied by a unique rule or function. One can then imagine traversing that space, moving from one coordinate to another. Although this is an oversimplification, it can be useful to think about it this way when trying to parametrize and visualize the structure and connection to other rules in that space.
Once we start imagining the Ruliad as a space, having a sort of geometry, we can start attributing to it physical properties and formal analysis such as geodesics (shortest paths), maxima and minima, propagation speeds, and emergent features.
In-Depth
To take a much deeper dive, i recommend reading these papers written by Wolfram on the topic
The Concept of the Ruliad—Stephen Wolfram Writings
Why Does the Universe Exist? Some Perspectives from Our Physics Project—Stephen Wolfram Writings
Part 4 : Observation & Observer Theory
The properties of the Ruliad elicit another series of questions about how it can be perceived. That because, any subsystem of the Ruliad can only map surjectively onto it, then any subsystem that exists anywhere inside of this object will consolidate information about its structure.
This animation to the right illustrates these limitations.
Perception
The first statement we can make about what we are witnessing here, is that the rotation is some sort of illusion of our perception, since we can say that what is happening is a continuous translation of each coordinate, to other coordinates rather than a rotation. In general we can apply this argument to any transformation.
Merging Behaviour
A second, and equally profound statement can be made here : That when points overlap to the same coordinate, the object's geometry gets occluded from our point of view, where one can no longer perceive it’s true geometry. Take note of what this means on a mathematical level : In a 2d coordinate system, several points will share the same coordinate IE: (2,3), (2,3), (2,3)... In a 3d coordinate system those points may actually be (2,3,1), (2,3,4), (2,3,8), but we can not be sure exactly which value the third parameter might be. From our point of view we simply do not have enough information about its structure without changing our perspective.
Observers perceiving the object from different perspectives will fail to fully resolve the underlying data structure that is actually there, because we are forced to consolidate information about it. This consolidation of information is equivalent to the merging behaviour of the hypergraph evolution in the Wolfram Model, and therefore it is this limitation that allows many observers to perceive the same fundamental laws of physics.
Equivalent Descriptions
Lastly, we conclude that from many different viewpoints, we could describe this underlying object in several different, but equally meaningful ways. In section 2 : The Wolfram Model, we find that this property of consolidation by observers in one form or another, is responsible for our description physics as we currently know it, and sets the basis for Wolfram’s view that other observers can potentially have completely different descriptions for the same underlying physical laws that are equally valid.
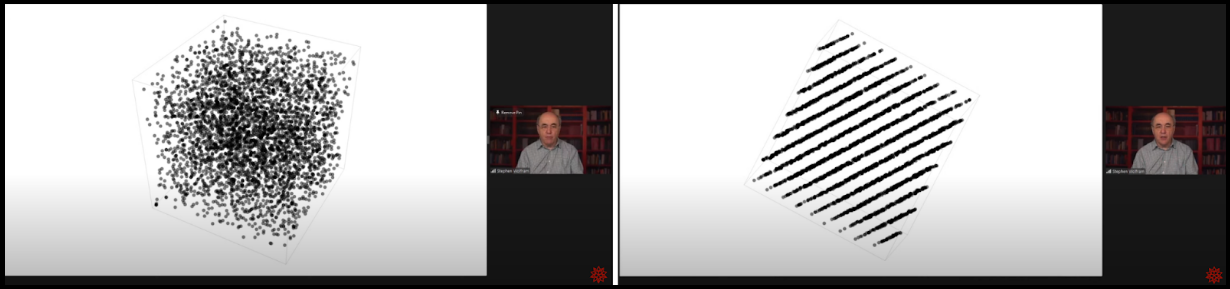
“Consider a quite random cloud of points. If we just turn this particular cloud of points to a particular angle, here’s what we will see. Obvious regularities…We had a bunch of points that are seemingly randomly distributed in a box, then we rotate the box and suddenly we see that these points lie on a bunch of planes, and we can see that this is a series of stripes.”
Excerpt from : Stephen Wolfram: Can AI Solve Science? - Stephen Wolfram Time Stamp 29:10 - 31:45
Extrapolate
If we imagine the infinitely complex structure of the Ruliad as an object similar to the animation, then there will be an infinite number of such viewpoints and as such any given sub-structure, from nearly any given viewpoint will be computationally irreducible. In that same token there will also be an infinite number of regularities that can be gleaned from those viewpoints.
It’s worth mentioning that time is also a data structure subject to this property, where the perception of time by any observer embedded in this object is limited. That will play a crucial role in the formal description of the Wolfram Model in the next section.
In-Depth
Stephan Wolfram has a lecture that explores observer theory in depth, that i highly recommend watching to get the full picture.
Stephen Wolfram on Observer Theory
Part 5 : The Wolfram Model
With New Kind of Science, The Ruliad and Observer Theory under your belt, you are now prepared and properly equipped to understand the weight and importance of the Wolfram Model.
Space
The Wolfram Model begins by stating that space is made of discrete information structures called “Atoms of Space.” They have no properties other than that they are unique, and that they have relationships to each other. Atoms are represented by nodes, and relationships are represented by edges that connect those nodes together. This forms a network graph, and more precisely a hypergraph, which generalizes this representation.
Rewrite Operations
We then introduce the dynamics of the model, which is to apply rewrite operations, rules that change a set of nodes and edges, into another set of nodes or edges For instance :

Whenever there is a relationship that has the form “XY” it changes to “XYZ” at no particular time. In other words this relationship…this rule… just eternally exists, such that all relations change in this way.
That’s pretty much the Wolfram Model in a nutshell! Everything is made of space. Everything else that happens from here on out, is a consequence of observers embedded in this model, and how they perceive the evolution of its structure.
Time & Relativity
As previously shown, there is not yet a notion of time. Rewrite operations just “are,” anywhere they apply, and so you can imagine that if this is the case, then the hypergraph should just apply all of these operations at once. For an observer that knows everything about the graph, this would be true (The infinite Ruliad-like observer), but once we embed our finite selves into this graph, we become forced to make decisions on which events must come before others in a causal order.
Taking the XY -> XYZ example again, we must force the constraint that XY needed to happen before XYZ happens, since XYZ depends on XY, for an observer that can only see a finite number of these operations occur at a time.
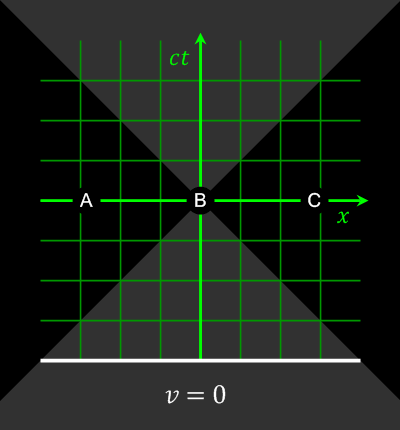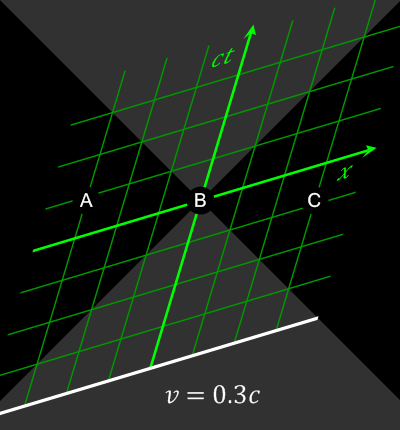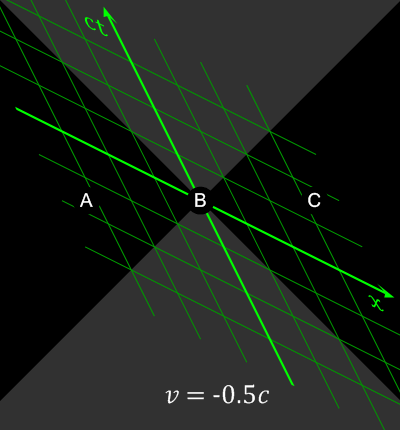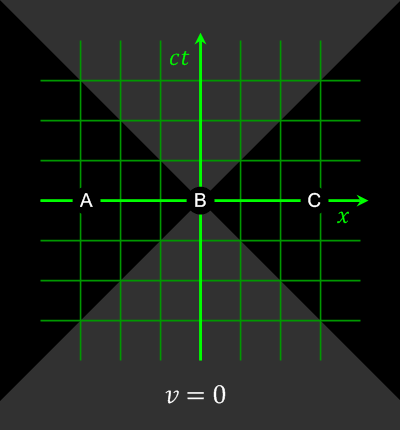
In the large limit, this structure forms the notion of directed time (causality) for an observer: That in order for an event to happen, a previous event must have had already happened. We also start to see how this ambiguity in the structure from an observer's perspective creates the notion of relativity : That if we have two or more of these operations that occur in two different places, say XY -> XYZ over here, and XY - XYZ over there, we have to perceive these in a causal order…where one of those events has to come prior to the other one, and that, depending on where you are embedded in this evolution determines which one happened for them first! (Relativity of Simultaneity)
Quantum Mechanics
Another property of this evolution that we are forced to obey as a consequence of embedding ourselves into it’s structure, is the ambiguity of possible rule operations that could have occurred.
For example, we have some output “=4” : There are a number of equally valid functions that could lead to this same result…1+3, 2+2, 10-6 and so on…
As it would turn out, these possible rewrite operations that could happen to the data structure, are all valid, and what an observer gets to distinguish as having happened, are the ones where different inputs converge to the same outputs as determined by the causal order. We depict this interplay as a branchial multi-way graph. As shown earlier in the observer theory section,this is the merging behaviour, and it governs quantum mechanics. It not only branches out into many different possible outcomes but also merges outcomes together because we as observers consolidate information about the underlying data structure.
Big Picture
In summary, Relativity, Quantum Mechanics and Thermodynamics all result from the ambiguity of observing the Ruliad object, because we as observers are forced to sequentialize and consolidate the hypergraph evolution in some way!
We can model all these ambiguities as multi-way graphs or spaces. Branchial Space is the geometry of those branching and merging events in the hypergraph evolution…a multiway causal graph is the geometry of the causal order of the hypergraph evolution…Rulial space is the space of rules and so on…The Wolfram Model heavily implies, that all systems can be modeled as Wolfram models and have geometries and properties of this kind. This is why you might hear Wolfram often, talk about relativistic effects and particles in say an economic system.
“The analog of particles in Rulial space, are concepts”
All of these representations are descriptions…slices…samplings of the Ruliad object. It is our view of its geometry.
Full Introduction
A broad all encompassing overview of the Wolfram Physics Model.
Wolfram Physics Project Launch
Technical
For those that are looking to go beyond the beginner, more conceptual introduction here and into technical details, Here are links to several important resources.
Introduction: Wolfram Physics Project Technical Background
Wolfram Physics I: Basic Formalism, Causal Invariance and Special Relativity
Wolfram Physics II: Emergent Hypergraph Geometry and General Relativity
Wolfram Physics III: Completion Procedures and Basic Quantum Mechanics"
Wolfram Physics IV: Multiway Invariance and Advanced Quantum Mechanics
Part 6 : Ruliology
Ruliology might sound like an unusual name, but it actually makes a lot of sense. Similar to how Biology is “The study of organisms” or how Geology is “The study of Earth…”
Ruliology is the study of rules.

The job is rather straightforward and simple : Run rules, and see what they do. That is Ruliology. Picture in your imagination, that you have an encyclopedia, where there is a page for each rule, you document it’s properties, what other rules it might be similar to and what things that rule could be used for…in the same way you might have a rock where you talk about its physical properties, it’s appearance, or how it reacts to other materials.
In another valid interpretation of Ruliogy, you might imagine something more like a genealogy rather than an encyclopedia, Where one depicts an ancestry that displays the relationships between different rules, reminiscent of Multiway Graphs, or the Tree of Life.
But what is a rule? What does it mean to run one? And how do we run them?
A rule is a symbolic abstraction, and operationally, you can think of a rule as an input/output interface. To run a rule, means to exercise the abstraction, such that you have some input, and some kind of instruction that changes the input, into the output.
If I have a red apple in my hand, and in front of me a machine, that turns red apples into green apples, then collectively the red apple [input], the machine with the instruction [instruction], and the green apple [output] is the running of a rule.

This machine need not be made out of metal, nuts or bolts. The machine could be…the funny caterpillar on your window sill that through whatever cellular mechanism turns the red apple into a green apple.
This example is the tip of the iceberg as you can imagine. The extent to which you can give an input a set of instructions to produce an output is one of the key ideas behind todays modern computer revolution. A rule can be as long and complex, or as short and as elegant as you can imagine. They can make perfect sense…or they might make no sense at all. They can be formal and rigorous, or natural and creative. In Step 7 - Multi-computation, we talk a bit more about the extent of this variability in rules and what they can be capable of.
In summary, this is the purpose of Ruliology…to explore the infinite landscape of possible rules that exist, and then just, see what they do. Documenting how they work, and how they might be meaningful to us.
Ruliology: Linking Computation Observers and Physical Law by Dean Rickles, Hatem Elshatlawy, Xerxes D. Arsiwalla
Part 7 : Multi-Computation
If one takes the idea of Computational Equivalence to its logical conclusion, then Ruliology, the study of rules, ultimately means that what every rule does is essentially “everything” since all rules are computationally equivalent to that of a Turing Universal Machine. For Ruliology, it isn’t meaningful to write on each page of the aforementioned encyclopedia that every rule “does everything.” This is where Multi-computation steps in to provide operational meaning to Ruliology and a more powerful way to think about and exploit the properties of this framework to model systems, create technology and do science.
The idea of Multi-Computation is to imagine every system as a sort of black box abstraction, where the system is computationally irreducible. Unlike Computational Reducibility which seeks to reduce systems down into a shorter description, Multi-Computation is a sort of inverse approach that seeks to map and explore all possible descriptions. The best way to do this is with a multi-way graph, but let's stick to Black Boxes for now.
This black box has the answer to any question you wish to ask it, like an oracle…the system can, with some input, do a computation that could give you any output, if only you knew the right initial condition…the right program. Perhaps that program is the silly caterpillar on the windowsill from earlier. Maybe it is some model of rule 30 or it could be a highly sophisticated humanoid, with a complicated procedure.
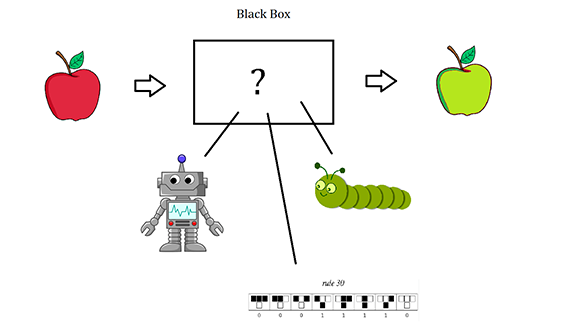
The problem of finding the answer to your question, is how to navigate the “infinite landscape” inside of this black box. Multi-computation is a mapping of this landscape, and how to navigate it is an exercise in doing observation…in doing “observer theory.”
Let’s take another example to show why this is a meaningful and powerful procedure. You can imagine this page as a “mini-ruliad” where the words and all it’s information exist eternally all at once to us. However in order for us to process the information content of this page, one has to lumber through each word in sequence, one at a time. This is the modern computational paradigm where one has to process things in a single order.
But imagine instead, that you were an army of ants that could do an operation on each word at the same time.You would be able to process the information content of this page all at once, almost as if it were like looking at an image or a painting. We’ve gone from looking at a sequential form of computation, to a non-sequential, much more powerful form of computation. Rather than lumbering through one thread of time, we are exploring many, if not all threads of time in this mini-ruliad, and we did this by simply changing our perspective to a new one…this leads to an important conclusion about how these ideas are connected together : the act of change in perspective is an exercise in running a rule (the operation done by the ants).
Multi-Computation therefore gives rise to a reunification with Ruliology despite their aforementioned incongruence : We study rules and what they do, so that we can give ourselves new perspectives that take advantage of either the Computationally reducible properties, or the computationally irreducible properties of systems, and we do multi-computation in order to map and explore the computationally irreducible landscape.

Reading a book in less than a few seconds as if it were like a painting on the wall, is like a super power, a term Wolfram often implies when discussing this paradigm. Computationally Irreducible processes contain a lot of power (arguably, the power of the entire universe), because it is the ability to program any system, to compute any computable function:
"If we want machine learning to be able to do the best it can, and perhaps give us the impression of “achieving magic”, then we have to allow it to show computational irreducibility."
Excerpt from : Stephen Wolfram Readings: What’s Really Going On in Machine Learning? Some Minimal Models - Stephen Wolfram Time Stamp 1:38:43 - 1:38:53
Part 8 : Impact
The Wolfram Model has an unprecedented impact on a multitude of areas, far beyond just physics. From Philosophy, to Economics, Biology, and Graphics Programming... Like stated in Section 5, and as we will again state below, in principle all systems can be modeled as Wolfram Models, or at least be meaningfully described in this framework. So take the initiative and apply the framework to your own fields of study, or research area, and see how they might apply there. In this step, we provide just a few of the implications to get you started.
Computational Equivalence and Intelligence
Principle of Computational Equivalence implies that intelligence is an equivalent concept between all systems, capable of doing things as sophisticated as we do. Concepts like IQ are more about “finding computational reducibility.” which makes sense…we’ve built our world on identifying computationally reducible parts of it, but this is not necessarily what it means to be intelligent, when we consider the power of Computational irreducibility.
Applicability of Wolfram Models
The Wolfram Model implies that all systems can be modeled as wolfram models, and described by this computational framework. As such, the wolfram model and this framework applies to any and all sciences and technological applications.
Science & Technology as an Exploration
The Wolfram Model implies that science is an exploration of an infinite landscape, similar to art we just create the things that we want to create. That doing science is an exercise in programming the universe.
Part 9 : Philosophical Implications
Ocean of Unlimited Potential
The Principle of Computational Equivalence and the existence of the Ruliad imply that the universe is synonymous with “an infinite ocean of potential” that we have access to through abstraction. That “what doesn’t exist” and “what does exist” is a very blurry line. This is a significant shift in world view, about the nature of reality.
Energy & the End of the Universe
The Wolfram Model and the existence of the Ruliad implies that energy is an illusory concept. That the universe contains an infinite amount of it, accessible through abstraction. It is proposed by Wolfram that the universe might not end in Heat Death, because to another more sophisticated observer, the universe will still “be interesting” to them.
Stephen Wolfram | How Universal Is the Idea of Numbers? | NUMEROUS NUMEROSITY 2021
Timestamp: 1:50:00 - 1:54:43
Universal Consciousness & Animism
The Principle of Computational Equivalence implies that boundaries between systems are illusory, and that we are all sharing or dipping into this same object (the Ruliad) for our behaviour which would mean that the universe is a sort of singular consciousness (universal consciousness), or from another point of view that all systems in nature are at some level conscious (animism).
Joshua Bach also has a similar break down of this philosophical viewpoint.
Seminar | Joscha Bach | Can we understand consciousness using the paradigms of AI?
Timestamp: 28:38 - 34:06
Part 10 : Relation to other Research Areas
The purpose of this section is to recognize how other popular areas of research are similar to, or are related to the Wolfram Model, in an attempt to bridge the gap and discover how one might apply the Wolfram Model to these other research areas.
Micheal Levin
Levin asserts that systems are intelligent universal machines, are forms of collective intelligences, navigating morphologic spaces to solve problems.
Michael Levin | Cell Intelligence in Physiological and Morphological Spaces
Gerard T'Hooft
T’hooft has put this theory aside in favor of ADS/CFT, but this interpretation of Quantum Mechanics remains subject to study, and its possible relation to the Wolfram Model.
The Cellular Automaton Interpretation of Quantum Mechanics - Gerard 't Hooft
Fotini Markopoulou
In this lecture, Fotini imagines space-time as a discrete network model.
Fotini Markopoulou on QUANTIZATION
Leonard Susskind
Well known physicist Leonard Susskind talks about Computational Complexity in Black Holes as well as holography.
Nima Arkani-Ahmed
Known for his work on Scattering Amplitudes and his Spacetime is Doomed lectures, Nima's work on Amplituhedron show a combinatorial structure with similiar properties to simple computational, combinatorial rules with respect to the calculation of scattering amplitudes. His Space Time is Doomed lectures also allude to emergent space-time, which is what the Wolfram Model also proposes