Perturbed Cellular Automaton: Difference between revisions
No edit summary |
No edit summary |
||
| (6 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
A perturbed cellular automaton represents a cellular automaton, but with changes to any number of cells in its state, that are not specified by the rules. | A [https://resources.wolframcloud.com/FunctionRepository/resources/PerturbedCellularAutomaton/ perturbed cellular automaton] represents a cellular automaton, but with changes to any number of cells in its state, that are not specified by the rules. | ||
[[File:Pca.jpeg|350px|thumb|right|Rule 30 with the red arrow indicating a perturbed cell that was changed from black to white, which results in a different pattern in the third row.]] | [[File:Pca.jpeg|350px|thumb|right|Rule 30 with the red arrow indicating a perturbed cell that was changed from black to white, which results in a different pattern in the third row.]] | ||
In his research, Stephen Wolfram has used this | In his research<ref>Stephen Wolfram, "Towards a Computational Formalization for Foundations of Medicine", Stephen Wolfram Writings, 2025, https://writings.stephenwolfram.com/2025/02/towards-a-computational-formalization-for-foundations-of-medicine/.</ref>, Stephen Wolfram has used this to model the medical concepts of disease and treatment. | ||
In these cases, Wolfram's idea is that the unperturbed automata represents a "healthy organism", and a perturbation represents an unpredictable change in the environment. If the perturbation results in a change to some specific feature of the automata that is considered to be deleterious, say, making it "die out”, then we imagine that perturbation as causing a “disease”. | In these cases, Wolfram's idea is that the unperturbed automata represents a "healthy organism", and a perturbation represents an unpredictable change in the environment. If the perturbation results in a change to some specific feature of the automata that is considered to be deleterious, say, making it "die out”, then we imagine that perturbation as causing a “disease”. | ||
| Line 9: | Line 9: | ||
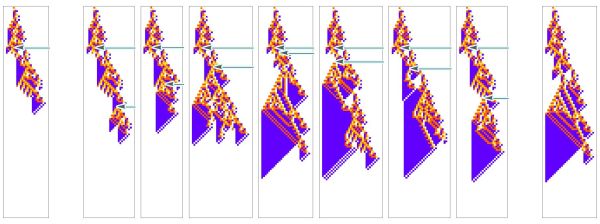
[[File:Abstractfigure.jpeg|600px|thumb|center| Perturbed cellular automata as a model for disease. In the first panel from the left, we show an unperturbed cellular automaton, our model for a “healthy organism”. In the subsequent panels, we show the resulting automata if we change one cell in the pattern, indicated by the light-blue arrow.]] | [[File:Abstractfigure.jpeg|600px|thumb|center| Perturbed cellular automata as a model for disease. In the first panel from the left, we show an unperturbed cellular automaton, our model for a “healthy organism”. In the subsequent panels, we show the resulting automata if we change one cell in the pattern, indicated by the light-blue arrow.]] | ||
In this framing Wolfram can begin to categorize the "types of disease": with some perturbations having little effect on the organism, other perturbations affecting the details of the pattern but keeping a similar overall shape, and some that disrupt both the "low-level" details and the "high-level" features, leading to unbounded "tumor-like" growth. | In this framing Wolfram can begin to categorize the "types of disease": with some perturbations having little effect on the organism, other perturbations affecting the details of the pattern but keeping a similar overall shape, and some that disrupt both the "low-level" details and the "high-level" features, leading, for example, to unbounded "tumor-like" growth. | ||
We can then imagine some secondary perturbation that is applied in an attempt to recover the original pattern, or “treat the organism”. | We can then imagine some secondary perturbation that is applied in an attempt to recover the original pattern, or “treat the organism”. | ||
Latest revision as of 00:02, 16 April 2025
A perturbed cellular automaton represents a cellular automaton, but with changes to any number of cells in its state, that are not specified by the rules.
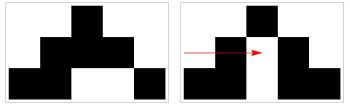
In his research[1], Stephen Wolfram has used this to model the medical concepts of disease and treatment.
In these cases, Wolfram's idea is that the unperturbed automata represents a "healthy organism", and a perturbation represents an unpredictable change in the environment. If the perturbation results in a change to some specific feature of the automata that is considered to be deleterious, say, making it "die out”, then we imagine that perturbation as causing a “disease”.
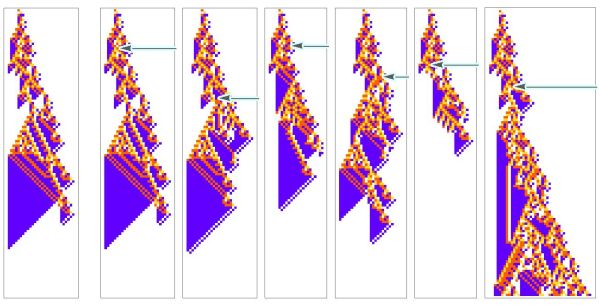
In this framing Wolfram can begin to categorize the "types of disease": with some perturbations having little effect on the organism, other perturbations affecting the details of the pattern but keeping a similar overall shape, and some that disrupt both the "low-level" details and the "high-level" features, leading, for example, to unbounded "tumor-like" growth.
We can then imagine some secondary perturbation that is applied in an attempt to recover the original pattern, or “treat the organism”.
- ↑ Stephen Wolfram, "Towards a Computational Formalization for Foundations of Medicine", Stephen Wolfram Writings, 2025, https://writings.stephenwolfram.com/2025/02/towards-a-computational-formalization-for-foundations-of-medicine/.