Perturbed Cellular Automaton: Difference between revisions
No edit summary |
No edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 3: | Line 3: | ||
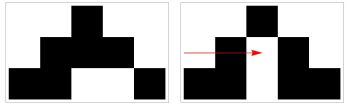
[[File:Pca.jpeg|350px|thumb|right|Rule 30 with the red arrow indicating a perturbed cell that was changed from black to white, which results in a different pattern in the third row.]] | [[File:Pca.jpeg|350px|thumb|right|Rule 30 with the red arrow indicating a perturbed cell that was changed from black to white, which results in a different pattern in the third row.]] | ||
In his research<ref>Stephen Wolfram, Towards a Computational Formalization for Foundations of Medicine, Stephen Wolfram Writings, 2025.</ref>, Stephen Wolfram has used this to model the medical concepts of disease and treatment. | In his research<ref>Stephen Wolfram, "Towards a Computational Formalization for Foundations of Medicine", Stephen Wolfram Writings, 2025, https://writings.stephenwolfram.com/2025/02/towards-a-computational-formalization-for-foundations-of-medicine/.</ref>, Stephen Wolfram has used this to model the medical concepts of disease and treatment. | ||
In these cases, Wolfram's idea is that the unperturbed automata represents a "healthy organism", and a perturbation represents an unpredictable change in the environment. If the perturbation results in a change to some specific feature of the automata that is considered to be deleterious, say, making it "die out”, then we imagine that perturbation as causing a “disease”. | In these cases, Wolfram's idea is that the unperturbed automata represents a "healthy organism", and a perturbation represents an unpredictable change in the environment. If the perturbation results in a change to some specific feature of the automata that is considered to be deleterious, say, making it "die out”, then we imagine that perturbation as causing a “disease”. | ||
Latest revision as of 00:02, 16 April 2025
A perturbed cellular automaton represents a cellular automaton, but with changes to any number of cells in its state, that are not specified by the rules.
In his research[1], Stephen Wolfram has used this to model the medical concepts of disease and treatment.
In these cases, Wolfram's idea is that the unperturbed automata represents a "healthy organism", and a perturbation represents an unpredictable change in the environment. If the perturbation results in a change to some specific feature of the automata that is considered to be deleterious, say, making it "die out”, then we imagine that perturbation as causing a “disease”.
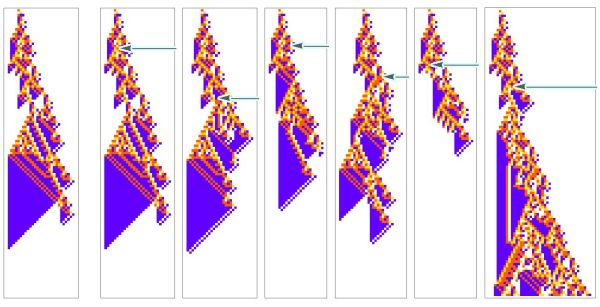
In this framing Wolfram can begin to categorize the "types of disease": with some perturbations having little effect on the organism, other perturbations affecting the details of the pattern but keeping a similar overall shape, and some that disrupt both the "low-level" details and the "high-level" features, leading, for example, to unbounded "tumor-like" growth.
We can then imagine some secondary perturbation that is applied in an attempt to recover the original pattern, or “treat the organism”.
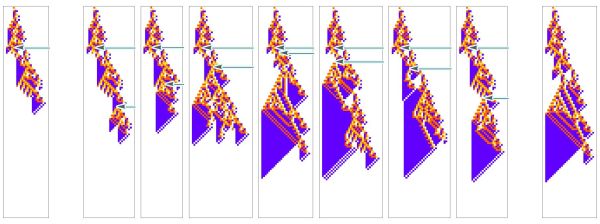
- ↑ Stephen Wolfram, "Towards a Computational Formalization for Foundations of Medicine", Stephen Wolfram Writings, 2025, https://writings.stephenwolfram.com/2025/02/towards-a-computational-formalization-for-foundations-of-medicine/.