Perturbed Cellular Automaton: Difference between revisions
No edit summary |
No edit summary |
||
| Line 9: | Line 9: | ||
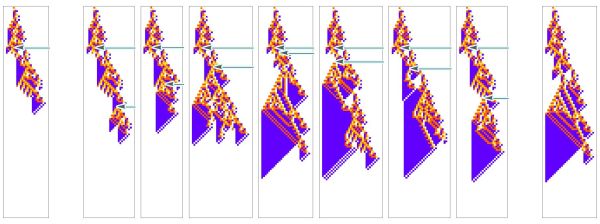
[[File:Abstractfigure.jpeg|600px|thumb|center| Perturbed cellular automata as a model for disease. In the first panel from the left, we show an unperturbed cellular automaton, our model for a “healthy organism”. In the subsequent panels, we show the resulting automata if we change one cell in the pattern, indicated by the light-blue arrow.]] | [[File:Abstractfigure.jpeg|600px|thumb|center| Perturbed cellular automata as a model for disease. In the first panel from the left, we show an unperturbed cellular automaton, our model for a “healthy organism”. In the subsequent panels, we show the resulting automata if we change one cell in the pattern, indicated by the light-blue arrow.]] | ||
In this framing Wolfram can begin to categorize the "types of disease": with some perturbations having little effect on the organism, other perturbations affecting the details of the pattern but keeping a similar overall shape, and some that disrupt both the "low-level" details and the "high-level" features, leading to unbounded "tumor-like" growth. | In this framing Wolfram can begin to categorize the "types of disease": with some perturbations having little effect on the organism, other perturbations affecting the details of the pattern but keeping a similar overall shape, and some that disrupt both the "low-level" details and the "high-level" features, leading, for example, to unbounded "tumor-like" growth. | ||
We can then imagine some secondary perturbation that is applied in an attempt to recover the original pattern, or “treat the organism”. | We can then imagine some secondary perturbation that is applied in an attempt to recover the original pattern, or “treat the organism”. | ||
Revision as of 23:44, 15 April 2025
A perturbed cellular automaton represents a cellular automaton, but with changes to any number of cells in its state, that are not specified by the rules.
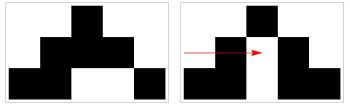
In his research, Stephen Wolfram has used this to model the medical concepts of disease and treatment.
In these cases, Wolfram's idea is that the unperturbed automata represents a "healthy organism", and a perturbation represents an unpredictable change in the environment. If the perturbation results in a change to some specific feature of the automata that is considered to be deleterious, say, making it "die out”, then we imagine that perturbation as causing a “disease”.
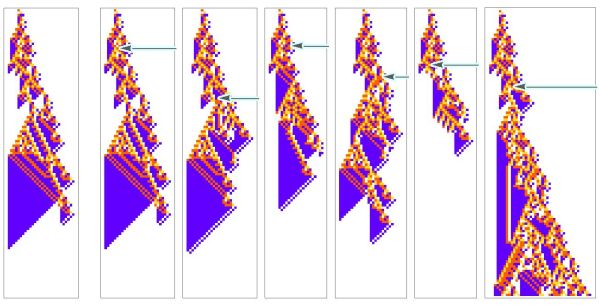
In this framing Wolfram can begin to categorize the "types of disease": with some perturbations having little effect on the organism, other perturbations affecting the details of the pattern but keeping a similar overall shape, and some that disrupt both the "low-level" details and the "high-level" features, leading, for example, to unbounded "tumor-like" growth.
We can then imagine some secondary perturbation that is applied in an attempt to recover the original pattern, or “treat the organism”.